Arveson’s hyperrigidity conjecture refuted by Bilich and Dor-On

Boom! This morning Boris Bilich and Adam Dor-On published a short preprint on the arXiv “Arveson’s hyperrigidity conjecture is false” in which they provide a counter example that refutes Arveson’s hyperrigidity conjecture. This is a fantastic achievement! It is one of the most interesting things that happened in my field lately and also somewhat of a surprise, a paper that is sure to make a significant impact on the subject.

(I should say that Adam was kind enough to let me read the manuscript a week ago, so that I had time already to check the details and as far as I can tell it looks correct.)

Let us recall quickly what the conjecture is (for more background see the series of posts that I wrote for the topics course I gave several years ago).

Let be a unital operator algebra generating a C*-algebra .

Arveson memorial article

Palle Jorgensen and Daniel Markiewicz have put together a beautiful tribute to the late Bill Arveson, with contributions from about a dozen mathematicians as well as a more personal piece by Lee Ann Kaskutas. This memorial article might appear later elsewhere in shorter form, but I think it would be interesting for many people to see the full tribute, with all the various points of view and pieces of life that it contains. I wrote a post dedicated to Arveson’s memory about half a year ago, where I put links to two recent surveys (1 by Davidson and and 2 by Izumi), and in about a month there will be a big conference in Berkeley dedicated to Arveson’s legacy; still I feel that this tribute really fills a hole, and conveys in broader, fuller way what a remarkable mathematician he was, and how impacted so many so strongly. Please share the link with people who might be interested.

William Arveson

William B. Arveson was born in 1934 and died last year on November 15, 2011. He was my mathematical hero; his written mathematics has influenced me more than anybody else’s. Of course, he has been much more than just my hero, his work has had deep and wide influence on the entire operator theory and operator algebras communities. Let me quickly give an example that everyone can appreciate: Arveson proved what may be considered as the “Hahn-Banach Theorem” appropriate for operator algebras. He did much more than that, and I will expand below on some of his early contributions, but I want to say something before that on what he was to me.

When I was a PhD student I worked in noncommutative dynamics. Briefly, this is the study of actions of (one-parameter) semigroups of *-endomorphisms on von Neumann algebras (in short E-semigroups). The definitive book on this subject is Arveson’s monograph “Noncommutative Dynamics and E-Semigroups”. So, naturally, I would carry this book around with me, and I would read it forwards and backwards. The wonderful thing about this book was that it made me feel as if all my dreams have come true! I mean my dreams about mathematics: as a graduate student you dream of working on something grand, something important, something beautiful, something elegant, brilliant and deep. You want your problem to be a focal point where different ideas, different fields, different techniques, in short, all things, meet.

When reading Arveson there was no doubt in my heart that, e.g., the problem classifying E-semigroups of type I was a grand problem. And I was blown away by the fact that the solution was so beautiful. He introduced product systems with such elegance and completeness that one would think that this subject has been studied for the last 50 years. These product systems were measurable bundles of operator spaces – which turn out to be Hilbert spaces! – that have a group like structure with respect to tensor multiplication. And they turn out to be complete invariants of E-semigroups on 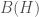. The theory set down used ideas and techniques from Hilbert space theory, operator space theory, C*-algebras, group representation theory, measure theory, functional equations, and many new ideas – what more could you ask for? Well, you could ask that the new theory also contribute to the solution of the original problem.

It turned out that the introduction of product systems immensely advanced the understanding of E-semigroups, and in particular it led to the full classification of type I ones.

So Arveson became my hero because he has made my dreams come true. And more than once: when reading another book by him, or one of his great papers, I always had a very strong feeling: this is what I want to do. And when I felt that I gave a certain problem all I thought I had in me, and decided to move on to a new problem, it happened that he was waiting for me there too.

I wish to bring here below a little piece that I wrote after he passed away, which explains from my point of view what was one of his greatest ideas.

For a (by far) more authoritative and complete review of Arveson’s contributions, see the two recent surveys by Davidson (link) and Izumi (link).