Advanced Analysis, Notes 16: Hilbert function spaces (basics)
by Orr Shalit
In the final week of the semester we will study Hilbert function spaces (also known as reproducing kernel Hilbert spaces) with the goal of presenting an operator theoretic proof of the classical Pick interpolation theorem. Since time is limited I will present a somewhat unorthodox route, and ignore much of the beautiful function theory involved. BGU students who wish to learn more about this should consider taking Daniel Alpay’s course next semester. Let me also note the helpful lecture notes available from Vern Paulsen’s webpage and also this monograph by Jim Agler and John McCarthy (in this post and the next one I will refer to these as [P] and [AM] below).
(Not directly related to this post, but might be of some interest to students: there is an amusing discussion connected to earlier material in the course (convergence of Fourier series) here).
1. Hilbert function spaces
A Hilbert function space on a set is a Hilbert space
which is a subspace of the vector space of all functions
, with one additional and crucial property:
For every the functional of point evalution at
, given by
, is a bounded functional on
.
This crucial property connects between the function theoretic properties of as a space of functions, and the Hilbert space structure of
and therefore also the operator theory on
. Hilbert function spaces are also known as reproducing kernel Hilbert spaces (RKHS), for reasons that will become clear very soon.
When we say that is a subspace of
, we mean two things: 1)
is a subset of
; and 2)
inherits its linear space structure from
. In particular, the zero function is the zero element of
, and two elements of
which are equal as functions are equal as elements of
.
Example: Perhaps the most interesting examples of Hilbert function spaces are those that occur when is an open subset of
, and now we’ll meet one of the most beloved examples. Let D denote the open unit disc in the complex plane
. Recall that every function
analytic in D has a power series representation
. We define the Hardy space
to be the space of analytic functions on the disc with square summable Taylor coefficients, that is
This space is endowed with the inner product
(*)
Before worrying about function theoretic issues, note that the space of formal power series with square summable coefficients is obviously isomorphic (as an inner product space) to when endowed with the inner product (*). But if a formal power series has square summable coefficients then its coefficients are bounded, so it is convergent in the open unit disc. Thus
is a space of analytic functions which as an inner product space is isomorphic to
, and is therefore complete.
To show that is a Hilbert function space on D, we need to show that for every
, the functional
is bounded. Well, if this functional is bounded, then by the Riesz representation theorem there exists some
such that
. Take another look at (*), recall that
, and putting these two things together it is not hard to come up with the guess that
. Since
, we have that
, so
. Plugging
in (*) we see that
, so that this functional is indeed bounded.
There are a great many other Hilbert function spaces of rather different function theoretic nature. Some of them are mentioned and studied in [P] and in [AM].
Example: The Hilbert space is a space of functions from
to
, and point evaluation is clearly bounded. Thus
is a Hilbert function space on set
. I have never heard of anything useful that came out of this point of view.
Exercise A.1: The Bergman space is the space of all analytic functions in the disc which are square integrable on the disc:
(where denotes the space of functions analytic in D). Show directly (that is, not by guessing the kernel functions) that point evaluation is bounded.
Exercise A.2: The Segal-Bargmann space is the space of all entire functions for which
. Show that this space is a Hilbert function space.
2. Reproducing kernels
Let be a Hilbert function space on a set
. As point evaluation is a bounded functional, there is, for every
, an element
such that
for all
. The function
is called the kernel function at
. We define a function on
by
The function is called the reproducing kernel
or simply the kernel of
. The terminology comes from the fact that the family of functions
enable one to reproduce the values of any
via the relationship
. Note that
.
Example: The kernel function for is
Exercise B: What is the kernel function of ? What about the Bergman space
? What about the Segal-Bargmann space?
The kernel has the following important property. If
and
, then
It follows that for every choice of points , the matrix
is positive semi-definite. A function with this property is called a positive definite kernel (sometimes it is called a positive semi-definite kernel, but let us lighten terminology). Every Hilbert function space gives rise to a positive definite kernel — its reproducing kernel. In fact, there is a bijective correspondence between positive definite kernels and Hilbert function spaces.
Theorem 1: Let be a positive definite kernel on
. Then there exists a unique Hilbert function space
on
such that
is the reproducing kernel of
.
Remark: Let me be a little bit more precise regarding the uniqueness statement, because in the context of Hilbert space one might mistakingly understand that this uniqueness is up to some kind of Hilbert space isomorphism. The existence statement is that there exists a subset of the space
of all functions on
, which is a Hilbert function space, and has
as a reproducing kernel. The uniqueness assertion is that this set
is uniquely determined.
Proof: Denote . Let
be the linear subspace of
spanned by the functions
. Equip
with the sesquilinear form
From the definition and the fact that is a positive definite kernel, the form
satisfies properties 2–4 from the definition of inner product (see Definition 1 in this post). That is, it is almost an inner product, the only property missing is
. As mentioned before (see Theorem 2 in that same old post) this means that the Cauchy-Schwartz inequality holds for this form on
. From this it follows that the space
is a subspace, and also that
for all
and
. This implies that the quotient space
can be equipped with the inner product
As usual, we are using the notation to denote the equivalence class of
in
. That this is well defined and an inner product follows from what we said about
. Now complete
to obtain a Hilbert space
.
We started with a space of functions on , but by taking the quotient and completing we are now no longer dealing with functions on
. To fix this, we define a map
by
(**)
This is a linear map and it is injective because the set spans
. Note that
(***) .
We may push the inner product from to
, and we obtain a Hilbert space of functions in
. Point evaluation is bounded by definition (see (**)), and the kernel function at
is
. By (***), this
. Let us now identify between
and
. It follows that
is spanned by the kernel functions
. The kernel function of this Hilbert function space
is given by
as required.
Now suppose that is another Hilbert function space on
that has
as a reproducing kernel. By definition, the kernel functions are contained in
, and since
is spanned by the kernel functions,
. However, if
is in the orthogonal complement of
in
then
for all
, thus
. This shows that
, completing the proof.
Remark: Sometimes Hilbert function spaces are referred to as reproducing kernel Hilbert spaces (RKHS for short), this terminology being justified by the preceding discussion.
Exercise C: Let be a RKHS with kernel
. Let
. Show that the matrix
is strictly positive definite (meaning that it is positive semi-definite and invertible) iff the functions
are linearly indendent, iff the evaluation functionals at the points
are linearly independent as functionals on
.
Exercise D: Show how the proof of the above theorem is simplified when is assumed strictly positive definite (meaning that the matrix
is strictly positive definite for any choice of points). Show how at every stage of the process one has a space of functions on
.
Exercise E: Rewrite the above proof of the theorem (for not necessarily strictly positive) so that it involves no quotient-taking and no abstract completions.
3. 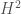 as a “subspace” of
as a “subspace” of 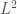
We now continue to study the space , and give a useful formula for the norm of elements in this space.
Let . For any
denote
. The power series of
is given by
This series converges to uniformly on the closed unit disc. In fact,
extends to an analytic function on a neighborhood of the closed unit disc, and the series converges uniformly and absolutely on a closed disc that is slightly larger than the unit disc. It follows that the following computations are valid:
It would be nice to say that for every
and this is almost true, but we have to be careful because elements in are not defined on
. However,
and this tends to as
by the dominated convergence theorem. In particular
We will use this formula below. Much more is true in fact: the functions converge almost everywhere to a function
, and
. Moreover,
can be identified via the map
with the subspace of
consisting of all functions with Fourier series that are supported on the non-negative integers: if
, then
. For details, see [AM]. What we will need is a little weaker fact:
Fact: A function analytic on D is in
if and only if
Proof: We already showed that functions have this property. Now let
be analytic in the disc, and suppose it has power series representation
. As before
By the monotone convergence theorem the right hand side converges to , so the limit of integrals is finite if and only if
.
4. Multiplier algebras
Let be a Hilbert function space on
, to be fixed in the following discussion. Now we define a class of natural operators on
.
The multiplier algebra of , denoted
, is defined as
In this definition simply denotes the usual pointwise product of two functions:
. For every
we define an operator
by
It is not unusual to identify and
, and we will do so too, but sometimes it is helpful to distinguish between the function
and the linear operator
.
Proposition 2: For all , we have
.
Proof: Obviously is a well defined linear operator. To show that it is bounded we use the closed graph theorem. Let
, and suppose that
. Since point evaluation is continuous we have for all
and
thus for all
, meaning that
, so the graph of
is closed.
Thus, is a subalgebra of
. We norm
by pulling back the norm from
(this means
), and this turns
into a normed algebra. We will see below that it is a Banach algebra.
Important assumption: In fact, there is a situation when is not a norm, but only a semi-norm. This doesn’t arise when for every
there exists a function
such that
. Thus we will assume this henceforth. This assumption holds in most (but not all) cases of interest, and in particular in the case of
. It is equivalent to the assumption that
for all
.
One of the instances when it is helpful to distinguish between a multiplier and the multiplication operator
that it induces is when discussing adjoints.
Proposition 3: Let . For all
, the kernel function
is an eigenvector for
with eigenvalue
. Conversely, if
is an operator such that
for all
, then there is an
such that
for all
and
.
Proof: We let and compute for all
but . Thus
.
For the converse, suppose for all
. Define
. For all
, we have
too. We now compute
It follows that , so
. It also follows that
.
Corollary 4: contains only bounded functions, and
.
Proof: This follows from the Propositions 2 and 3, since the eigenvalues of are contained in
, which is contained in the disc of radius
.
Corollary 5: is closed in the weak operator topology of
, and, in particular,
is a Banach algebra.
Remark: The weak operator topology is the topology on in which a net
if and only for all
,
. The reader may safely replace this with the norm topology of
for the purposes of these lectures.
Proof: If is a net in
converging to
in the weak operator topology, then
WOT. Then for all
,
converges weakly to
, so
is an eigenvalue for
. By Proposition 3,
.
Example: Let’s find out who is the multiplier algebra of . Since
, we have that
, and in particular every multiplier in
is an analytic function on D. By Corollary 4 we have that every multiplier is bounded on the disc. Thus
The right hand side denotes the algebra of bounded analytic functions in D. On the other hand, by the formula developed in Section 3, we have for and
,
By the fact at the end of Section 3, we obtain and
, so
and
.
Exercise F: What is the the multiplier algebra of ? Of
? Can you cook up a non-trivial RKHS that has a trivial (scalars only) multiplier algebra?
5. First magic trick
Note that as a consequence of the previous example and Corollary 5 we have that is a Banach algebra. It follows readily that the limit of any locally uniformly convergent sequence of analytic functions (on any open set) is also analytic. I leave it to the reader to check just how much complex analysis we used to obtain this result, and to compare with the other proof they know of this fact.
[…] first that is a multiplier. Then by Proposition 3 in the previous post extends to and is equal to . Let and . […]
Interesting post. It has taken me some time to arrive.
I may return to it in the future, but let me say a few things:
1. It seems that there are 2 minor typos: in line 9 in Section 1 and also 3 lines above Exercise F.
2. As for the magic trick: I can’t say for sure what is used and not from the theory of functions, but note that along the way the existence of the complex exponent function, together with some of its elementary properties (e.g., the existence of the period ), are used. The proofs of these properties, although elementary (basing, e.g., elementary calculus and complex analysis), are not so trivial. Besides, can you make the proof of Corollary 5 a little bit more detailed? I guess that I simply miss something trivial, but still. Thanks!
), are used. The proofs of these properties, although elementary (basing, e.g., elementary calculus and complex analysis), are not so trivial. Besides, can you make the proof of Corollary 5 a little bit more detailed? I guess that I simply miss something trivial, but still. Thanks!
Thanks for the remarks. The typos area fixed.
As for the use of the function – you are right, one does require the existence of this function on
– you are right, one does require the existence of this function on ![[0, 2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C+2%5Cpi%5D&bg=fff&fg=444444&s=0&c=20201002) and the fact that it is periodic.
and the fact that it is periodic.
As for Corollary 5: If (a net) converges in the weak operator topology to
(a net) converges in the weak operator topology to 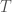 , then
, then  has the same eigenvectors as
has the same eigenvectors as  , so by Proposition 3,
, so by Proposition 3,  is an eigenvector for
is an eigenvector for  , and by Proposition 3 again
, and by Proposition 3 again  for some
for some  . This shows that
. This shows that  is closed in the weak operator topology. This, in turn, implies that this set is closed in the norm topology, because that topology is stronger.
is closed in the weak operator topology. This, in turn, implies that this set is closed in the norm topology, because that topology is stronger.
Finally, is clearly a subalgebra if
is clearly a subalgebra if 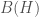 so closedness in norm implies that it is a Banach algebra. The norm in
so closedness in norm implies that it is a Banach algebra. The norm in  is defined as
is defined as  , so
, so  is Banach, too.
is Banach, too.
1. Thanks for the explanation. What is still not completely clear is how exactly you deduced that is an eigenvector of
is an eigenvector of  . However, maybe you did this by observing that
. However, maybe you did this by observing that 
 holds for all functions
holds for all functions  . In particular it holds for
. In particular it holds for  where
where 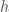 is the function satisfying
is the function satisfying  (assumed to exist in the important assumption above Proposition 3), hence implying that
(assumed to exist in the important assumption above Proposition 3), hence implying that  exists (and equals
exists (and equals  ). Finally, the above implies that the quality
). Finally, the above implies that the quality  holds for all
holds for all  and hence indeed
and hence indeed  , that is,
, that is,  is an eigenvector of
is an eigenvector of  .
.
2. There is a minor typo in one of the words used in line 3 of the proof of Corollary 5.
I also want to say a few words about my claim regarding the existence of the complex exponent function and its elementary properties, e.g., its period. This fact is not as obvious as one may think at first. One can define , which can be easily shown (Weierstrass M-test) to be well defined and infinitely many continuously differentiable, but the problem is now to show that this function does satisfy certain properties, e.g., having a period and having absolute value 1 when
, which can be easily shown (Weierstrass M-test) to be well defined and infinitely many continuously differentiable, but the problem is now to show that this function does satisfy certain properties, e.g., having a period and having absolute value 1 when  is imaginary. The proof is elementary but not so immediate.
is imaginary. The proof is elementary but not so immediate.
Apparently one can try to avoid such a proof by saying that and now we can use known properties of the trigonometric functions (we are actually interested in the case where
and now we can use known properties of the trigonometric functions (we are actually interested in the case where  is real for proving that this function, as a function from the whole real line to the complex plane, is periodic and has absolute value 1). But the problem is that these properties, as studied in first courses in calculus (and usually never revisit again!), are based on inherently circular proofs. For instance, in order to show that the trigonometric functions are differentiable one uses the limit
is real for proving that this function, as a function from the whole real line to the complex plane, is periodic and has absolute value 1). But the problem is that these properties, as studied in first courses in calculus (and usually never revisit again!), are based on inherently circular proofs. For instance, in order to show that the trigonometric functions are differentiable one uses the limit  whose proof is based on the fact that any portion of the circle has a well defined length, but in order to define such a length one needs to assume that the trigonometric functions are continuously differentiable! Another problem: what is the precise definition of
whose proof is based on the fact that any portion of the circle has a well defined length, but in order to define such a length one needs to assume that the trigonometric functions are continuously differentiable! Another problem: what is the precise definition of 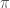 ? The root of this problem actually goes back to the classical geometry of the Greeks because lengths of curves and also measure of angles were not well defined there (one needs basic tools from calculus, in particular the notion of limit, in order to define them).
? The root of this problem actually goes back to the classical geometry of the Greeks because lengths of curves and also measure of angles were not well defined there (one needs basic tools from calculus, in particular the notion of limit, in order to define them).
A nice approach for getting out of this vicious circle is explained in [1, pp. 43-46]. It is based on elementary complex analysis and power series. Another approach, based on elementary integral calculus and the properties of the function (represented as an integral) is explained in [2, pp. 432-438].
function (represented as an integral) is explained in [2, pp. 432-438].
[1] L. V. Ahlfors, Complex analysis: An introduction to the theory of analytic functions of one complex variable, Second edition, McGraw-Hill Book Co., New York, 1966
[2] J. W. Kitchen, Calculus of one variable, Addison-Wesley, Reading, Mass, 1968
Let me also add that another problem in classical geometry is the definition of lengths of segments because the whole real line was not well understood at that time. But the previous mentioned problems (lengths of curves and the definition of measures of angles) seem to be more problematic even when one has a good definition of a length of a segment and some understanding of the real line. The Greeks also didn’t have a definition of areas of complex shapes (e.g., a disk), which is another major weak point.
Your remarks on the circularity of the definitions of the trigonometric are in place. However, I have to object to the comments that the Greeks did not have a well defined notion of length, angle, area. etc. Of course, they did not have what we would subjectively call “well defined”, but certainly their notions were clear, useful and correct. Certainly there is no reason to hold the Greeks up to our contemporary (and not eternal) standards. Even today, there is room for viewing mathematics that way.
Do know anything about implications of invariance subspace problem? In Peter Lax’s book he says that it is still an open question whether the problem itself is interesting. Are any other conjectures connected to this.
I don’t know any results that go like: “Assume that every bounded operator acting on an infinite dimensional separable Hilbert space has an invariant subspace. Then…”
It is plausible that some kind of structure theorem for operators will be developed after the invariant subspace problem is solved (in the affirmative), but it is hard to believe that a general existence theorem of an invariant subspace will yield a very effective and useful structure theorem.
However, it is even harder to believe that this problem will be solved (either way) without immensely increasing our understanding of operators on Hilbert space, and techniques developed for that problem will surely find their way to tackle other problems.
That is a nice joke of Peter Lax, but for me there is no question that the problem itself is interesting.
As a final comment for today, let me say that the theory of reproducing kernels has some interesting and important applications. For instance, it has been used (in the finite dimensional case) by Steve Smale and his group at the City University of Hong Kong for solving (to some extent) important problems in computational biology. Smale gave a series of talks at IMPA in October 2012 about this issue. The first 3 talks can be found in the first link below and the last one in the second link.
Remarks:
I. There are some surprises in talks 2,3,4.
II. There are other nice talks in the links below (with additional surprises).
III. Warning: one may need to download the whole video file (approximately 500MB) in order to watch it since online streaming may be bad.
[Link 1] http://www.impa.br/opencms/pt/institucional/memoria_impa/Videos/palestras.html
[Link 2] http://video.impa.br/index.php?page=2012—impa-60-anos
Thanks for all the comments!
[…] a natural example of a Hilbert space, for example, then try looking at Hilbert function spaces (see these notes). Arguably, the Hardy space is as natural as you can hope that an infinite dimensional space will […]
[…] with the notion of Hilbert function spaces – also called reproducing Hilbert spaces (see this post for an introduction). Suppose that is a Hilbert function space on a set , and its reproducing […]
[…] See this linked post for an introduction to the theory of reproducing kernel Hilbert spaces. You need to read that (if you don’t know this stuff), in order to continue reading. […]
[…] in reproducing kernel Hilbert spaces (aka Hilbert function spaces) – see this old post for a crash introduction to the subject. ) The theory of reproducing kernel Hilbert spaces makes a connection between function theory, on […]